Постановка задачи: Используя Решатель, найти

Постановка задачи: Используя Решатель, найти решение системы линейных уравнений AX = B
Решение системы уравнений как линейных, так и нелинейных нетрудно сформулировать как оптимизационную задачу в постановке, требуемой Решателем. Пусть имеется система уравнений:
F1(X) = 0; F2(X) = 0; … Fn(X) = 0;
Для Решателя эта задача естественным образом формулируется так:

вектор переменных X представляет массив регулируемых ячеек;
функции FI(X) задают ограничения типа равенств;
в качестве целевой функции можно выбрать, например, Ф(X) = SUM(FI(X)). При этом можно выбирать любой критерий для целевой функции, устремляя ее к минимуму, максимуму или требуя нулевое значение для Ф(X).

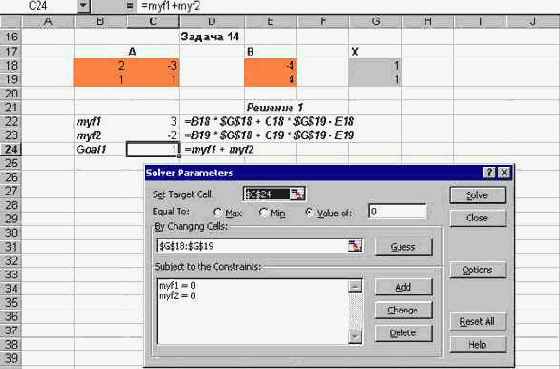
В качестве примера я использовал те же данные, что и в задаче 12. Взгляните, как выглядит постановка этой задачи в окне Решателя:

увеличить изображение
Рис. 2.14. Постановка задачи в окне Решателя
А вот как выглядит решение, найденное Решателем:

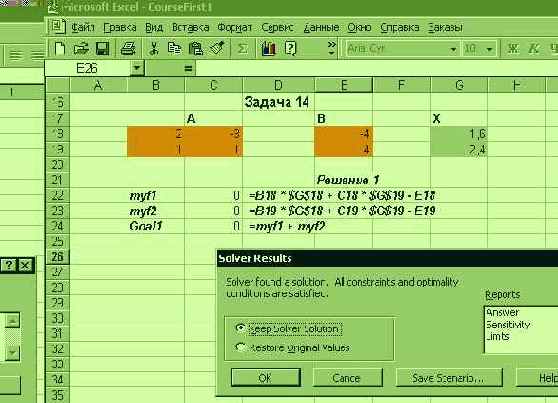
Рис. 2.15. Решение системы линейных уравнений, найденное Решателем

Постановка задачи: Используя Решатель, найти решение системы линейных уравнений AX = B
Решение системы уравнений как линейных, так и нелинейных нетрудно сформулировать как оптимизационную задачу в постановке, требуемой Решателем. Пусть имеется система уравнений:
F1(X) = 0; F2(X) = 0; … Fn(X) = 0;
Для Решателя эта задача естественным образом формулируется так:

вектор переменных X представляет массив регулируемых ячеек;
функции FI(X) задают ограничения типа равенств;
в качестве целевой функции можно выбрать, например, Ф(X) = SUM(FI(X)). При этом можно выбирать любой критерий для целевой функции, устремляя ее к минимуму, максимуму или требуя нулевое значение для Ф(X).

Рис. 2.15. Решение системы линейных уравнений, найденное Решателем
Нужно понимать, что когда используется Решатель, многое зависит еще и от того, как сформулирована задача. Решатель допускает различные постановки одной и той же задачи, а также имеет ряд параметров, позволяющих управлять процессом решения. Так, при решении системы линейных уравнений можно, например, рассматривать задачу как задачу минимизации следующей функции:
Ф(X) = F12 (X) + F22 (X) + … +Fn2 (X) -> Min
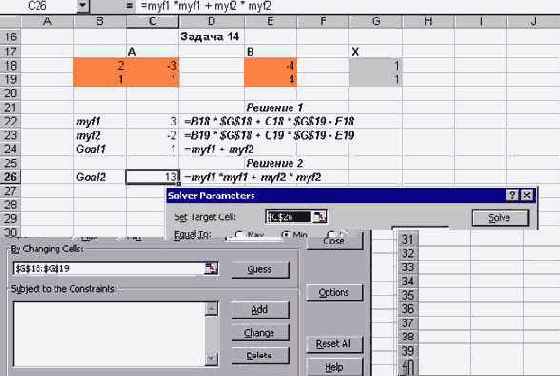
При минимизации этой функции можно и не задавать ограничения. Понятно, что решение системы исходных уравнений является точкой минимума целевой функции Ф(X). На следующих рисунках показана постановка задачи и ее решение для этого варианта постановки:

увеличить изображение
Рис. 2.16. Второй вариант постановки задачи

увеличить изображение
Рис. 2.17. Решение, найденное Решателем, во втором варианте
Как видите, в обеих постановках Решатель успешно находит решение системы линейных уравнений. Чтобы убедиться, что "проклятие размерности" не так уж и страшно Решателю, я провел еще один эксперимент, выбрав задачу большей размерности, и стал искать решение системы из пяти линейных уравнений. На рабочем листе Excel я задал:

матрицу коэффициентов этой системы - myA;
вектор правых частей - myB;
вектор переменных - SolX5
в ячейках Myl1-Myl5 формулы, задающие соответствующие линейные уравнения. Фактически, я ввел одну формулу в ячейку myl1: {=СУММ(B30:F30*SolX5) -I30}

Затем скопировал ее в соседние ячейки. При копировании автоматически изменяется диапазон ячеек, который указывает на следующую строку матрицы коэффициентов, и изменяется ссылка на ячейку, задающую правую часть уравнения.
В ячейки с именами MYST и MYST1 я ввел формулы для целевых функций, соответствующих двум различным постановкам: =Myl1 + Myl2 + Myl3 + Myl4 + Myl5; = Myl1* Myl1 + Myl2* Myl2 + Myl3* Myl3 + Myl4* Myl4 + Myl5* Myl5;
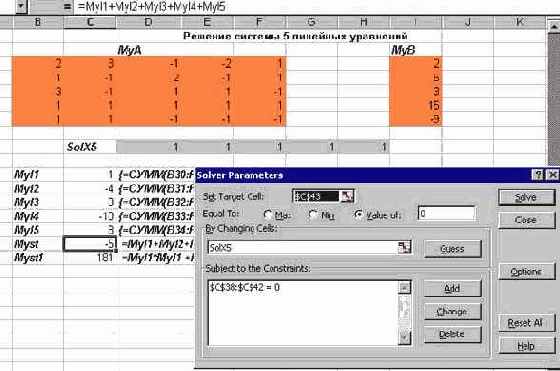
В первом случае целевая функция линейна, но задаются дополнительные ограничения. Во втором - минимизируется квадратичная функция при отсутствии ограничений. Диалоговое окно Решателя в момент задания его параметров при оптимизации первой целевой функции выглядит так:

увеличить изображение
Рис. 2.18. Постановка задачи линейного программирования
Обратите внимание на некоторые детали постановки задачи. В окне изменяемых ячеек я задал имя вектора решений - SolX5. Вектор ограничений распространяется на весь диапазон уравнений, но формально задан в виде одного векторного ограничения. Перед тем, как приступить к решению, я изменил настройку параметров Решателя. Взгляните, как выглядит окно Options (Параметры), в котором производится настройка:

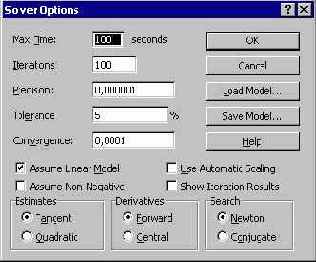
Рис. 2.19. Настройка параметров Решателя
Как видите, возможностей управлять решением достаточно много, и я еще позже поговорю о них подробнее. Сейчас же замечу, что я оставил без изменения максимальное время, отводимое на решение - 100 секунд, максимальное число итераций - 100, требуемую точность выполнения ограничений - 0, 0000001. Единственное, что я сделал, это включил флажок Linear, указав, что в данной постановке Решатель имеет дело с задачей линейного программирования, поскольку все ограничения и целевая функция линейно зависят от переменных задачи.
Точное решение нашей системы уравнений задается вектором (1, 2, 3, 4, 5). Решатель нашел это решение.

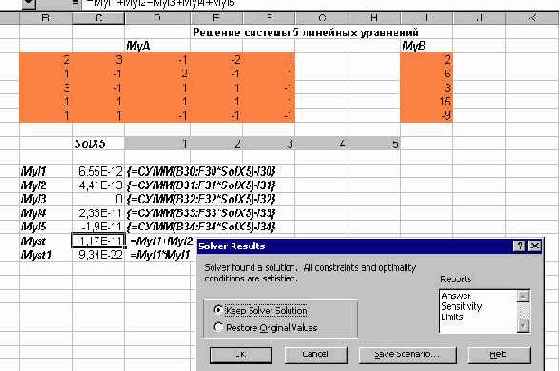
увеличить изображение
Рис. 2.20. Решение системы 5 линейных уравнений с линейной целевой функцией
Я получил также решение этой задачи и для квадратичной целевой функции в различных постановках: с учетом ограничений, без их учета, минимизируя или требуя, чтобы функция принимала нулевое решение. Во всех случаях, поверьте, Решатель не подкачал.

Содержание раздела